Neste artigo falaremos sobre o teste t de Student, que é um teste de hipóteses utilizado quando queremos tirar conclusões de um grupo inteiro de indivíduos com base em apenas uma pequena amostra coletada. Esse problema pode parecer de um contexto muito específico, porém é mais comum do que se pensa.
O objetivo deste artigo é apresentar o teste de hipótese T de Student, carinhosamente chamado de teste t. Ao longo do texto, abordaremos o racional por trás da técnica, quais suas limitações e, por fim, um exemplo prático aplicando o caso mais básico: o teste t sobre a média de uma amostra.
Focaremos nos conhecimentos básicos, sendo este artigo recomendado para quem está tendo o primeiro contato com o tema e também para quem deseja relembrar algum conceito esquecido.
Glossário
Antes de avançarmos no conteúdo, vale recapitular alguns conceitos importantes que usaremos ao longo do artigo.
- Amostra: conjunto parcial de indivíduos de uma mesma população. Exemplo: os funcionários de apenas um setor.
- Amostragem aleatória: selecionar muitas amostras com elementos aleatoriamente escolhidos a partir de todos os elementos de uma população.
- Desvio padrão: a média da diferença entre a média amostral e cada elemento.
- Distribuição de Probabilidade (ou apenas Distribuição): descrição do comportamento de um fenômeno ocorrido em um grande número de repetições.
- Histograma: gráfico que representa a frequência de repetição de uma variável em uma amostra.
- Inferência: criar julgamentos sobre uma população a partir de uma amostra.
- Média: a soma dos valores divididos pela quantidade de valores.
- População: conjunto de indivíduos que compartilham uma característica. Exemplo: todos os funcionários de uma mesma empresa.
- Variância: desvio padrão ao quadrado.
Exemplos para entender a aplicação do teste t no dia a dia
Imagine que você está em transição de carreira e uma empresa quer te contratar. Ao pesquisar sobre ela em sites de avaliação, as notas e comentários são positivos: altos salários, boa cultura e empresa em crescimento. A empresa parece ser uma excelente oportunidade, e, por fim, você aceita o cargo.
Entretanto, foi só depois da admissão que você se deparou com outra realidade: o time promove um ambiente tóxico, salários estáticos e não há perspectivas de crescimento de carreira.
Um dos possíveis problemas desse cenário infeliz foi a consideração das notas e comentários existentes como aplicáveis para todas as áreas da empresa. Que bom seria se, toda vez que tomássemos uma decisão, tivéssemos em mãos todas as informações existentes. Apesar desse cenário quase nunca ser verdade, felizmente a estatística criou uma solução: o teste de hipótese T de Student.
Segunda situação
Imagine uma base cadastral de funcionários de uma empresa. A partir dela, é possível levantar hipóteses, por exemplo:
- “Mulheres e homens nos mesmos cargos recebem, em média, o mesmo salário?” ou
- “As pessoas da área Comercial costumam receber mais aumentos salariais que na área de Pesquisa e Desenvolvimento?”
Caso tivéssemos as bases completas (ou seja, população) tanto de quem está sendo comparado quanto da referência de comparação, bastaria calcular a média de ambos grupos. Pronto, simples! Porém, a tarefa torna-se mais complexa quando imaginamos um cenário onde apenas uma base incompleta, ou seja, de apenas alguns indivíduos (como amostra), está disponível.
Considerando o novo cenário, a comparação direta entre os diferentes grupos é errônea, pois podem existir indivíduos fora da amostra que contradizem o resultado da comparação. Esse segundo cenário, além de mais difícil, é o mais comum em nosso dia a dia. Assim, o problema consiste em: como tirar conclusões de um grupo inteiro com base apenas em uma amostra?

Como nasceu e o que é o Teste t de Student?
Depois de muito sofrer com o problema similar ao anterior, um cervejeiro inglês chamado William Sealy Gosset sugeriu em 1908 uma solução que ficou conhecida como teste de hipótese t de Student.
Gosset descobrindo o teste t, circa 1908
Texto alternativo: Homem com uma caneca de cerveja em uma mão e outra mão fazendo uma pose de vitória, comemorando algo.
Gosset, mais conhecido pelo homônimo Student, trabalhava na cervejaria Guinness e lidava com o seguinte problema: como avaliar a qualidade das toneladas e toneladas de grãos utilizados na cerveja com base em apenas uma pequena amostra?
Para dificultar sua vida, o problema deveria ser resolvido utilizando a menor quantidade possível de grãos, afinal de contas, quanto mais cerveja é testada, menos cerveja é produzida.
A solução adotada foi, essencialmente, comparar as médias entre os grãos, avaliando especificamente a qualidade média desejada para todo o lote e a qualidade média presente na pequena amostra.
A genialidade da solução, contudo, é que Gosset criou uma maneira de estimar a probabilidade dos grãos da amostra serem comparáveis ao seu lote inteiro, utilizando-se de estatística e um pouco de bruxaria.
O racional do teste t consiste nas seguintes etapas:
- Desejamos identificar a característica (por exemplo, qualidade) de uma população (como, lote de grãos), porém possuo apenas uma amostra (por exemplo, punhado de grãos).
- Conheço as características de uma população ideal (por exemplo, qualidade ideal).
- Conheço o perfil das diferentes amostras retiradas da população ideal.
- Comparo a probabilidade da amostra em mãos ser uma das muitas amostras possíveis originadas a partir de uma população ideal.
- Caso a probabilidade for baixa, concluo que a amostra não foi originada de uma população ideal.
“Mas como fazer deduções de uma coisa que não se conhece?”
Na estatística é possível avaliar um fenômeno e sua ocorrência através de um gráfico chamado distribuição de probabilidade. Ele registra os possíveis resultados de um fenômeno e sua frequência, sendo ilustrada em uma curva. Dentre os diferentes tipos de curvas resultantes da natureza, uma das mais comuns é a distribuição normal.

A capacidade de dedução do teste t é garantida pela distribuição normal, pois ela garante propriedades valiosas sobre a frequência, média e dispersão (isto é, variância) de um conjunto de dados.
O histograma apresenta um exemplo, ilustrando no eixo horizontal os elementos do conjunto, e no eixo vertical estão a frequência que cada elemento se repete:
Gráfico 1 – Distribuição Normal com média 0 e desvio padrão 1.
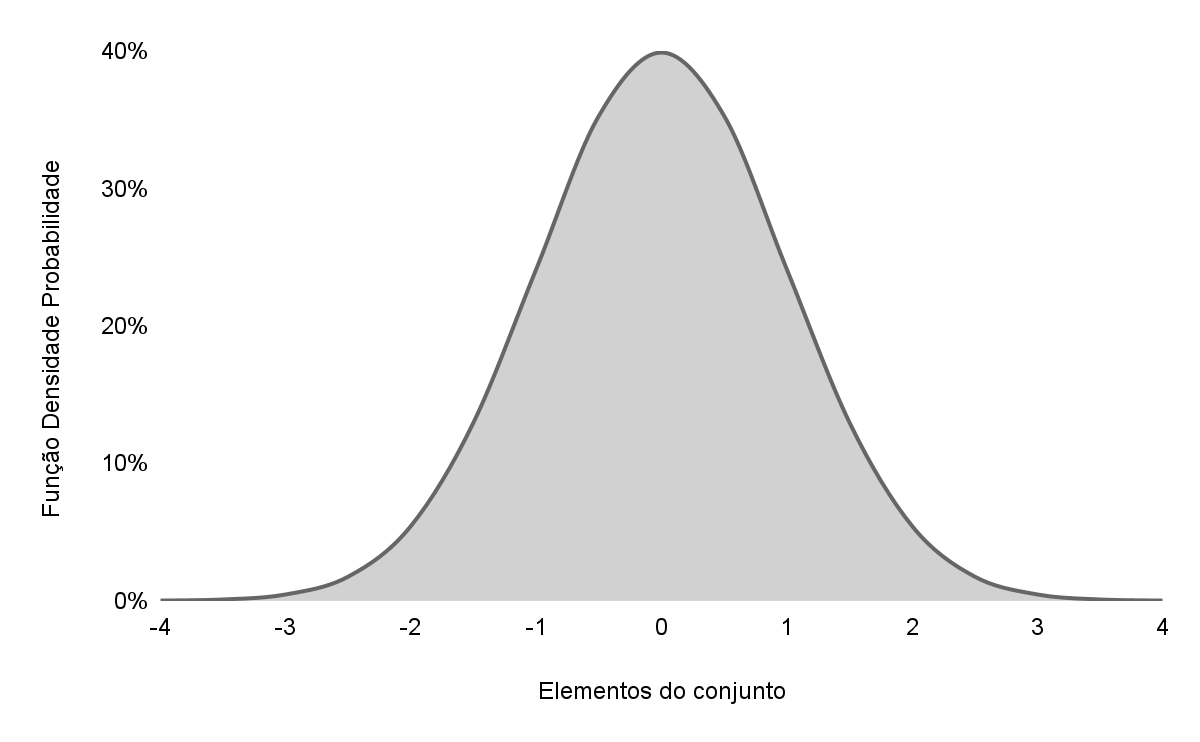
Observe na figura que as maiores frequências estão próximas à média 0, diminuindo na medida que se afastam e nunca chegando a uma frequência nula. Essas são duas propriedades importantes da distribuição normal: (1) maior frequência dos resultados próximos ao centro e (2) uma constante dispersão. Na imagem acima, observamos que o resultado 0 ocorre para aproximadamente 40% da amostra.
“E como ter certeza de que o fenômeno apresenta uma distribuição normal? Com o Teorema do Limite Central!”
De fato, como não temos acesso a base de dados completa, não sabemos inicialmente com que tipo de distribuição estamos lidando. Apesar disso, existe uma maneira de transformar praticamente todos os tipos de distribuição em normal. Para isso, utilizaremos o Teorema do Limite Central. Pela teoria:
“o teorema central do limite afirma que a média de uma amostra de n elementos de uma população tende a uma distribuição normal”
Em outras palavras, não importa qual distribuição estamos falando, caso considerássemos uma população qualquer e coletássemos diferentes amostras de um mesmo tamanho, poderíamos calcular a média de cada amostra e o conjunto dessas médias se comportaria como uma distribuição normal.
O processo de criar várias amostras diferentes de uma mesma população chama-se amostragem aleatória. É possível ver esse conceito acontecendo passo a passo neste site (em inglês), o qual ilustra a aplicação completa do Teorema do Limite Central.
Gráficos 2.1, 2.2 e 2.3 – Aplicação do Teorema do Limite Central em diferentes distribuições
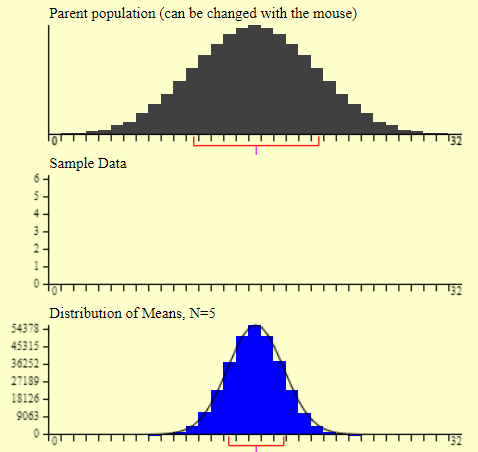
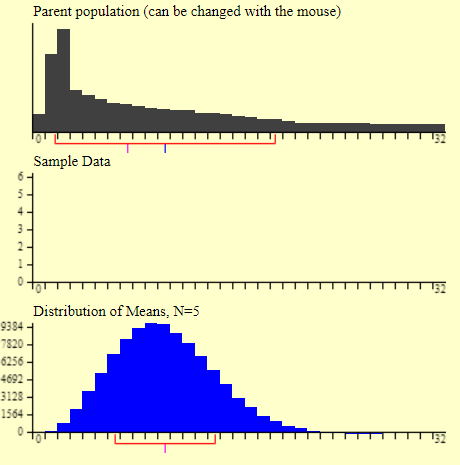
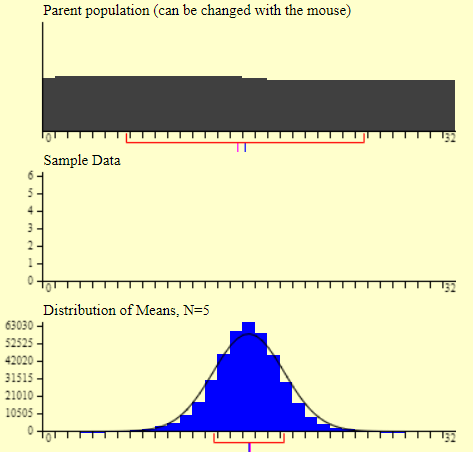
A sequência de imagens acima apresenta a aplicação do Teorema do Limite Central. As três imagens mostram em cinza diferentes tipos de curvas de distribuição. Logo abaixo, em azul, estão as distribuições resultantes da aplicação do Teorema do Limite Central. Repare que independente do formato inicial da curva, as distribuições convergem em um único formato.

Utilizando-se do Teorema do Limite Central, o conjunto das médias amostrais apresenta uma distribuição normal em torno da mesma média original. Dessa forma, garantimos a normalidade ao mesmo tempo que a média da distribuição resultante é a mesma da média original. Extremamente útil, não?
Apesar de simples na teoria, existe uma limitação para o Teorema do Limite Central. A principal dificuldade do teorema é que o tamanho das diferentes amostras retiradas da população deve ser grande. Atualmente existem várias “regras de bolso” que apontam o quão grande precisa ser o tamanho amostral, seja de 30, 120 ou até 500 elementos, como por exemplo este artigo. Em contrapartida, é consenso na literatura que, quanto mais parecida a distribuição original for de uma normal, menor é o tamanho amostral necessário para a aplicação do Teorema do Limite Central.
Adicionalmente, existem outros testes estatísticos que avaliam se uma determinada amostra pertence a uma população com distribuição normal. Esses testes, chamados de Testes de Normalidade estão fora do escopo deste artigo.
“Certo, consegui garantir a normalidade. E agora?”
Agora é a melhor parte. Uma vez que garantimos a normalidade, utilizaremos uma nova propriedade da distribuição normal: o volume de dados contidos nos intervalos determinados pela distância entre a média e os desvios padrões. Segundo a regra 68-95-99, os intervalos formados por:
- um desvio padrão contém 68% dos dados;
- dois* desvios padrões contém 95% dos dados;
- três desvios padrões contém 99% dos dados;
*Observação: mais precisamente 1,96 desvios padrões. Vamos falar mais sobre isso ainda no texto.
Gráfico 3 – Intervalos formados por desvios padrões
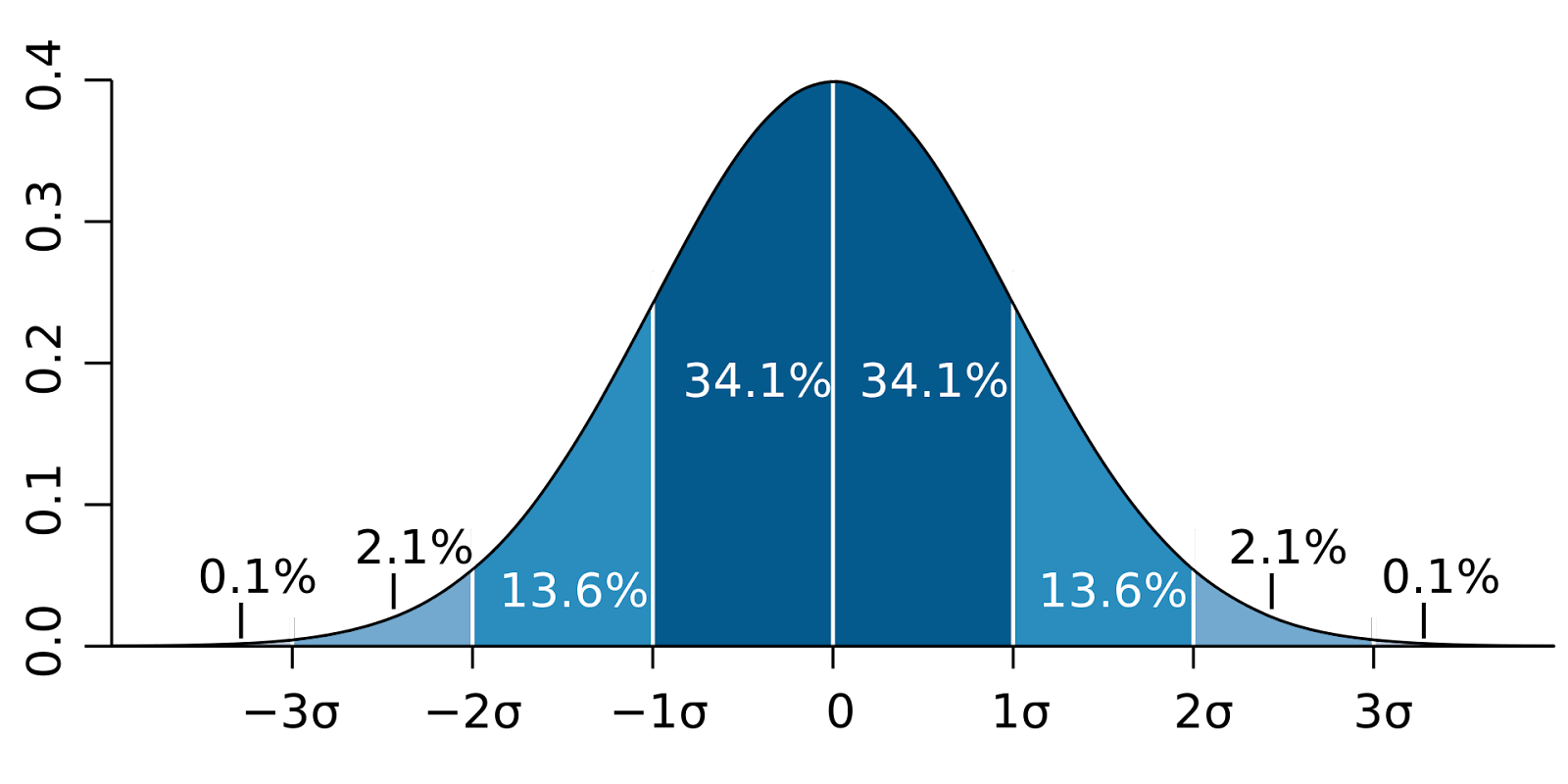
O gráfico ilustra os intervalos e como eles concentram grandes volumes dos dados da população. Na imagem, o símbolo σ representa desvio padrão, como exemplo, podemos ver que o intervalo formado pela distância de dois desvios padrões em relação a média, ou seja, as quatro fatias centrais do gráfico, somam 95%. Isso significa que caso sorteássemos um elemento dessa população 100 vezes, em média, 95 vezes o elemento estaria contido dentro desse intervalo.
Considerando o cenário original da cerveja, o próximo passo é escolher um tamanho amostral grande o suficiente para que o Teorema do Limite Central seja aplicável, o que, por sua vez, garantiria a normalidade da distribuição. Uma vez que os intervalos formados pelos desvios padrões concentram a maioria dos possíveis valores da amostra.
Dessa forma, o que nos resta é entender se a média amostral está dentro desse intervalo ou não:
Caso 1 – a média amostral está dentro do intervalo
Caso a média amostral esteja dentro do intervalo, ela faz parte de 95% das possíveis amostras criadas a partir da população ideal. Como a probabilidade é alta, não é possível rejeitar a possibilidade da amostra ter sido originada a partir da uma população de referência.
No cenário da cerveja, esse resultado significa que não há indícios estatísticos de que o lote inteiro de grãos testados seja de qualidade diferente da qualidade ideal.
Caso 2 – a média amostral está fora do intervalo
Caso a média amostral esteja fora do intervalo, ela faz parte dos 5% das possíveis amostras aleatórias. Como essa probabilidade é muito pequena, consideramos que o lote inteiro que deu origem ao punhado de grãos testados não tem a mesma qualidade ideal necessária para a produção, ou seja, rejeitamos a igualdade entre a população testada e a população de referência.
Uma outra maneira de explicar o resultado seria indicar que a amostra de grãos testada apresenta uma qualidade tão diferente da ideal, que a única explicação estatística é que o lote inteiro provavelmente também apresenta um nível diferente de qualidade.
Quantidade de desvios padrões
É importante ressaltar que a escolha da quantidade de desvios padrões fica a critério do freguês. A utilização de 1,96 (aproximadamente dois) desvios padrões é a prática mais comum em artigos científicos.
Na prática, o aumento da quantidade de desvios padrões aumenta o rigor do teste, pois se com dois desvios padrões nós rejeitamos apenas 5% dos casos, quando aumentamos o número de desvios padrões para três, passamos a rejeitar apenas 1% dos casos.

Matematicamente falando, utilizaremos a fórmula abaixo para metrificar em quantidade de desvios padrões o quão longe da média comparada nossa amostra está:

Como na prática, já que não possuímos o desvio padrão resultante da amostragem aleatória, utilizaremos uma estimativa baseada no desvio padrão amostral e o tamanho amostral:

No final das contas, é essa combinação entre Teorema do Limite Central e propriedades da distribuição normal que permitiu a Student fazer inferências sobre grandes populações contendo apenas pequenas amostras.

Exemplo prático: pesquisa de satisfação
Agora vamos ver o Teste T de Student na prática!
Anualmente uma empresa realiza uma pesquisa de satisfação. Em 2020, a nota média foi de 5,41. Porém, em 2020, infelizmente, houve um problema de comunicação e registrou-se apenas 50 respostas de funcionários aleatórios. As repercussões da não divulgação do resultado são graves e não há tempo para refazer a pesquisa.
Gráfico 4 – Histograma das 50 respostas da pesquisa 2021
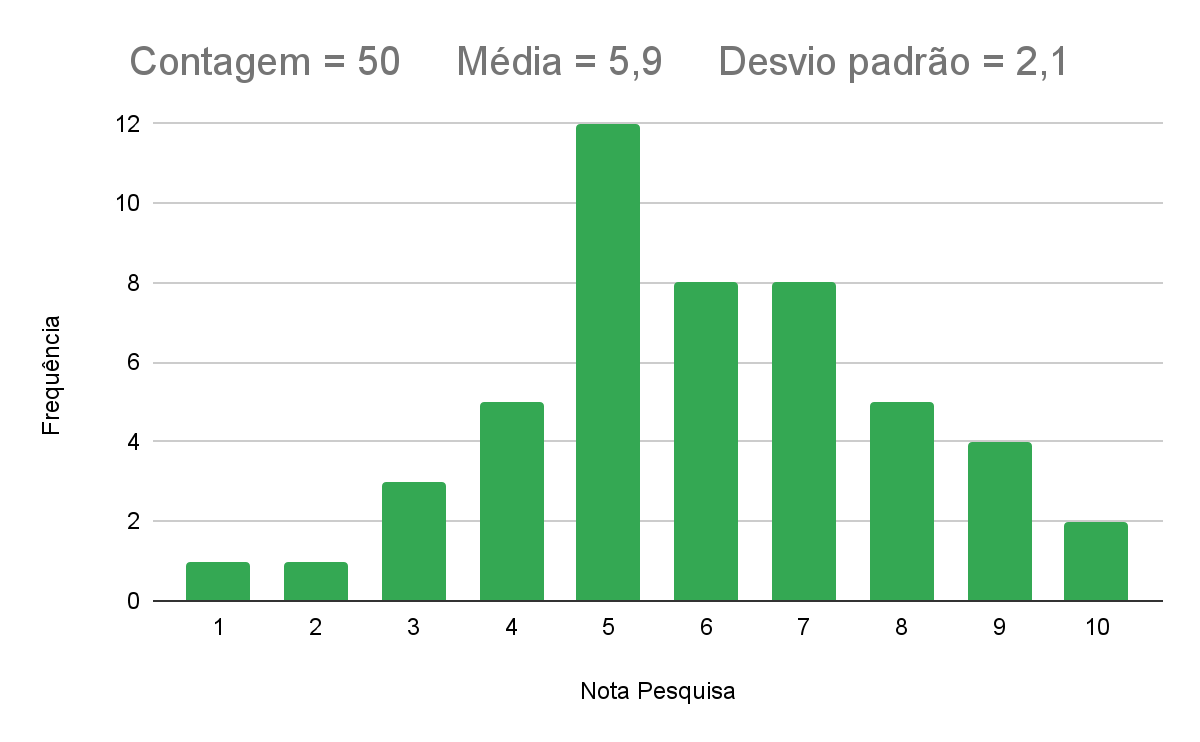
No histograma anterior, observamos que a média amostral é 5,94, nota média superior a 5,31 registrada em 2020. Apesar da quantidade amostral não ser alta, é razoável apontar que a distribuição observada na amostra apresenta forte similaridade com a distribuição normal.
Dessa forma, é razoável considerarmos que a pequena amostra de 50 elementos é suficiente para a aplicação do Teorema do Limite Central neste caso. Dadas as condições anteriores, faz sentido aplicarmos o teste t neste caso.
Aplicando a fórmula, temos

O valor t de 2,06 está fora do intervalo proposto que contém os 95% da amostra (i.e. intervalo de -1,96 e +1,96 desvios padrões). Desse modo, entende-se que a amostra tem apenas 5% de probabilidade de ter sido originada a partir da mesma população de de 2020, ou, em outras palavras, a amostra tem 95% de probabilidade de pertencer a uma população diferente de 2020..
Gráfico 5 – Comparação da distância entre Média Populacional e Média Amostral
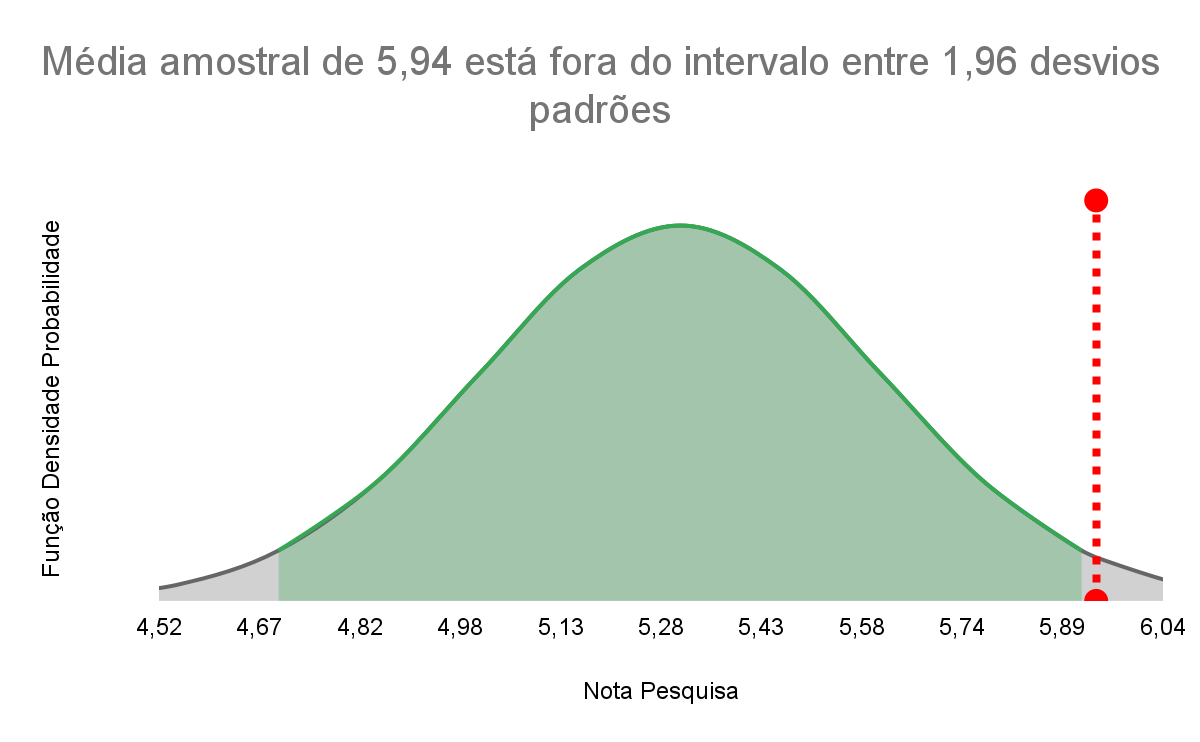
Portanto, podemos dizer que temos 95% de certeza de que a nota média de satisfação da empresa mudou de 2020 para 2021.
Próximos passos e limitações
O exemplo prático anterior avaliou as respostas de apenas um ano da pesquisa, porém é possível se deparar com casos em que precisaríamos comparar as respostas de vários anos de pesquisa. Repare que esse novo cenário é mais complexo, pois a quantidade de amostras a serem avaliadas aumenta. Felizmente, ainda é possível aplicar o teste t, pois existem variantes do teste que são adequadas para cenários diferentes.
É possível aplicar o teste t de Student em casos de:
- Distribuições monocaudais (distribuição que segue apenas para um lado)
- Distribuições menos parecidas com normais
- Duas ou mais amostras
- Amostras de tamanhos diferentes
- Amostras com desvio padrão diferentes
- Teste de normalidade para distribuições
É importante ressaltar que, apesar da relativa simplicidade e alta flexibilidade de aplicação, o teste t é capaz de identificar apenas a diferença, porém não consegue identificar de quanto é essa diferença.
No exemplo prático anterior, a conclusão é que a satisfação é diferente entre 2020 e 2021, porém não identificamos qual é a diferença de notas entre as pesquisas.
Conclusão
Neste artigo introduzimos de forma conceitual e prática o teste de hipótese T Student. Partindo de sua origem como um método de controle de qualidade da produção de cerveja na Guinness, passando pelos conceitos estatísticos chaves, distribuição normal e o Teorema do Limite Central. Após isso, seguimos por um caso prático e, por fim, enumeramos as diferentes variações possíveis do teste e também suas limitações.
O que achou do teste T de Student? Ficou com dúvidas? Já se viu em uma situação de usar ele em um projeto? Conta para a gente nos comentários e se quiser receber em seu e-mail mais conteúdos como este, assine a nossa newsletter!

Bibliografia
- Artigo original “The Probable Error of A Mean”, Student (1908).
- Hypothesis Testing: An Intuitive Guide for Making Data Driven Decisions.
- Regra 68-95-99,7.
- The Importance of the Normality Assumption in Large Public Health Data Sets
- The strange origins of the Student’s t-test – The Physiological Society
- The t-test and robustness to non-normality – The Stats Geek
- William Sealy Gosset – Wikipedia







